5 Number Summary Calculator | Five Number Summary Calculator

5 Number Summary Calculator

Enter the data separated by ,

No. Separated By:

$\color{white}Solution$

Getting the five number summary is very helpful when analyzing data sets, which is why we created the 5 Number Summary Calculator.

To use this calculator you must perform the following steps:

Select the separator that you will use to delimit the data, you can use commas, semicolons, spaces, tabs or one value per line.
Enter the values in the textarea using the separator selected in the previous step.
Press the calculate button to get the five numbers summary .

The solution offered by the calculator shows step by step how to calculate the 5 numbers summary. This is a great help to any student or teacher of statistics.

What is the 5 number summary?

The 5-number summary is one of the most widely used tools for exploratory data analysis, because it allows the shape of the distribution to be determined using basic mathematical operations.

The 5-number summary is made up of the following values:

Minimum value (x_{_min})
First quartile (Q_₁)
Median (Q_₂)
Third quartile (Q_₃)
Maximum value (x_{_max})

These five values have been selected because each of them reveals information about a part of the data set:

The median allows us to know where the mean value is.
The first and second quartiles show how spread out the data are.
The minimum and maximum values allow knowing the range of the data.

Integral definition

The easiest way to build a five-number summary is to first put the data in ascending order. Once this is done, it is easy to identify the smallest value, the three quartiles, and the largest value.

Below we present a series of examples to explain how to find the 5 number summary. These examples have been solved with the 5 number summary calculator.

Example 01: Consider a sample whose values are 20, 25, 28, 17, 30, 32, 27, 14, 18, and 25. Find the five-number summary of this data.

Example 01 - how to find 5 number summary

Example 02: Below are the sales, in millions of dollars, of 15 supermarkets. Find the five-number summary.

{15536, 19365, 1036, 4263, 3053, 8962, 2379, 726, 538, 809, 973, 5369, 9682, 7513, 1392}

Example 02 - how to find five number summary

What is an Indefinite Integral?

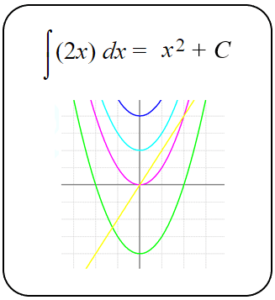
From what was explained above we can conclude that the function f(x) has infinite primitives, since if F(x) is primitive of f(x), so will any other function defined as G(x) = F(x) + C, where C is a constant value. The concept of indefinite integral is used to refer to the set of all antiderivatives of a function f(x).

For example, the indefinite integral of f(x)=2x is x²+C, which groups the family of primitive functions: x², x²+1, x²+2, x²+3, …

Definition of Definite Integral

The definite integral of a function f(x) determines the area under the curve on a closed interval [a, b].

⌠⌡
	b

	a

f(x) dx

Barrow’s Rule tells us that the definite integral of f(x) on the closed interval [a,b] is equal to the difference between the values that a primitive function F(x) takes on that interval. From this rule we obtain the formula for the definite integral:

⌠⌡
	b

	a

f(x) dx = F(b)−F(a)

Definite integral formula

Example: Calculate the definite integral of f(x)=x^2+3 in the interval [0, 2]:

Improper integral

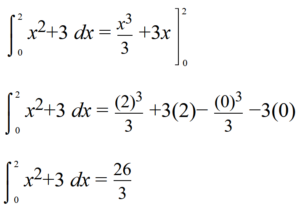
An improper integral is a special type of definite integral in which the function becomes undefined at some point in the interval of integration. This may be because one or both limits of integration are infinite, or because there is a point within the interval of integration at which the function does not exist.

There are three types of improper integrals:

Improper integrals of type 1 are those in which one or both limits of integration have an infinite value and the function is continuous on that interval.

Illustration of improper integrals of type 1

Improper integrals of type 2 are integrals that experience an asymptotic discontinuity in the interval of integration.
The improper integrals of type 3 are a combination of the previous two.

The Integral Solver that we present to you here is also a wonderful improper integral calculator with which you will be able to solve all kinds of improper integrals in a simple way.

Integration rules

The integration rules are a set of guidelines that help us to perform the integration of basic functions in a simple way. Here are the basic integration rules:

Integral power rule

⌠⌡xⁿ dx = xⁿ⁺¹n+1 +C

Integral of a constant

⌠⌡a dx = ax+C

Integration rule for e^x

⌠⌡e^x dx = e^x+C

Integration rule for a^x

⌠⌡a^x dx = a^xln(a) +C

Integral of 1/x

⌠⌡1x dx = ln(x)+C

Trig integral rules

⌠⌡sin(x) dx = −cos(x)+C

⌠⌡cos(x) dx = sin(x)+C

⌠⌡tan(x) dx = −ln(cos(x))+C

⌠⌡csc(x) dx = ln(tan(x/2))+C

⌠⌡sec(x) dx = ln(tan(x/2)+π/4)+C

⌠⌡cot(x) dx = ln(sin(x))+C

Properties of integrals

⌠⌡f(x)+g(x) dx = ⌠⌡f(x) dx+ ⌠⌡g(x) dx

⌠⌡f(x) − g(x) dx = ⌠⌡f(x) dx − ⌠⌡g(x) dx

⌠⌡k•f(x) dx = k⌠⌡f(x) dx, where k is a constant

5 Number Summary Calculator | Five Number Summary Calculator